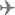 Data D : Atmosphere and Airspeeds Data D : Atmosphere and Airspeeds
 The performance and other operational characteristics of the
aircraft are directly influenced by the properties of the atmosphere in which it is
flying. These properties vary depending on weather conditions, seasons of the year,
geographical location and particularly with the height above the ground. In order to
standardise aircraft analysis, the International Civil Aviation Organisation (ICAO), in
agreement with other bodies, has specified an international standard for the atmosphere
(ISA). This is now established as the recognised basis for all aircraft analysis. In this
standard, height above sea-level is measured as the true (tape-line) distance (the
geometric altitude) assuming constant gravitational acceleration (g) with height (i.e. a
mean sea-level value go = 9.80665 m/sec2). This height definition is known as the
geopotential altitude.
The ISA recognises several altitude regions in which air
temperature is defined to be either constant or varying linearly with height. Only the
lowest two regions are applicable to current civil aircraft operations. The standard
defines the sea-level (quoted as SL and meaning zero altitude) air temperature as
288.15°K (15°C) and then assumes a linear variation with height up to 11 km (about 36089
ft) to a temperature of 216.65°K. This region is called the 'troposphere'. Most civil
aviation is flown in this region, or just above it, but as aircraft and engines become
more efficient higher altitudes (up to 40,000ft) will be used for optimum cruise
conditions.
Above 11 km and up to 20 km the ISA defines a constant
temperature with height (at 216.65°K). This constant temperature region is called the
'lower stratosphere'. Above this region the standard atmosphere assumes the temperature to
rise and then fall. Since even supersonic transport aircraft operate below 20 km altitude,
the upper stratosphere regions are not significant to civil operations.
In the lower regions The atmosphere in the lower regions is
assumed to follow normal gas laws. This means that temperature, pressure and density are
related by thermodynamic equations and functions. The relationships described on the next
page can be used for aircraft analysis
Temperature (Degrees Kelvin, °K)

In the operational altitudes appropriate to civil aircraft
the variation of temperature with height is defined in the ISA. From a specified sea-level
value it reduces linearly up to 11km and then remains constant. The equation defining
temperature in the troposphere (below 11km) has the following form:-
TALT = To - [L. h]
where: TALT = Air temperature (°K) at altitude
(h)
To = Air temperature at sea-level = 288.15 °K
L = 0.0065 °K/m
h = altitude (m), with maximum value of 11 Km.
In the lower stratosphere (above 11 km) the temperature
remains constant:-
TALT = 216.66°K.
Pressure (Pascal, Pa [= N/m2])

The variation of pressure with altitude is governed by the
gas equation shown below:-
PALT = Po [ TALT / To
] g/R.L
where PALT = pressure at altitude (h)
(Po = pressure at sea-level = 1011325 Pa)
g = gravitational acceleration = 9.81 m/sec2
(assumed constant)
R = universal gas constant = 287.3 J/kgK (assumed constant)
(Note: as the temperature is assumed to be constant in the
ISA the exponential
[g/RL] in the equation above has a constant value of
5.2561)
Density (kilograms per cubic metre)

The variation of density is directly related to temperature
and pressure through gas laws:-.
rALT = PALT
/ R.TALT
where: rALT = density at altitude h (kg/m3)
(ro = density at sea-level = 1.225 kg/m3)
Viscosity (kilogram per metre second)

Viscosity is needed to determine kinematic viscosity as
shown in the next item.
mALT = (1.458x10-6
x TALT3/2) / TALT
+ 110.4
where: mALT = viscosity (kg/ms) at altitude (h)
Kinematic Viscosity (square metre per second)

The coefficient of kinematic viscosity is used in
determination of Reynolds Number It is evaluated by the ratio:-
nALT = mALT
/ rALT
where: nALT = coefficient of kinematic viscosity
at altitude (m2/s)
Speed of Sound (metre per second)

The speed of sound varies with altitude by the following
relationship:-
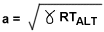
where: a = speed of sound at altitude (h) (m/s)
(ao = speed of sound at SL = 340.29 m/s)
g = coefficient = 1.4 (assumed constant in the ISA)
R as above
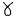 = 1.4 for air = 1.4 for air
Coefficients

Several non-dimensional coefficients are used in some of
the estimating procedures (e.g. engine performance). These are mainly ratios of the
conditions at altitude to the sea level (often ISA) values:-
Mach number (M) = V / a
where: V = aircraft true airspeed (m/s)
a = local speed of sound (m/s)
Atmosphere

The standard atmosphere approximates to the climatic
conditions at about 40°latitude North. To account for other conditions the international
standard committee recognised other standard climates (e.g. tropical maximum, arctic
minimum, temperate max and min.). It is normal practice not to predict these variations
from ISA but assume that the user directly inputs a temperature change to account for
local conditions (e.g. + 15°C for hot airport allowance when assessing take-off
performance). Such variations are shown in the graph below:-
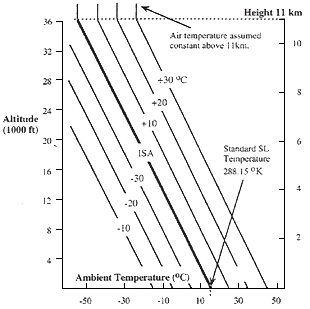
Note: that although the sea level temperature may vary from
the ISA condition,
the lapse rate (change in temperature with height) is
assumed to be constant at
0.0065 °K/m from all sea level (SL) temperature values.
Spreadsheet

All the atmosphere equations can be incorporated into a
spreadsheet to determine the ISA properties of the atmosphere at defined heights (h), see
below:-
Col A: Altitude (m) with initial (SL) value h = 0 and steps
at chosen intervals.
Col B: Ambient temp. (°K) with initial (SL) value TSL
= 288.15
then Th = 288.15 - 0.0065h
Col C: Temperature ratio q = Th / TSL
Col D: Ambient air pressure (N/m2) with initial
(SL) value PSL = 1011325
then Ph = PSL x q 5.2561
Col E: Relative pressure ratio d = Ph / PSL
Col F: Ambient air density (kg/m3) with initial
(SL) value rSL = 1.225
then rh = rSL. d/q
Col G: Relative density ratio s = rh / rSL
Col H: Speed of sound a = (1.4*287.3*Th)0.5
The estimation of the atmospheric properties at a
particular height and with temperature variation for ISA is done by inputting suitable
values to the spreadsheet:-
Airspeeds

Performance calculations are usually quoted at true
airspeed (TAS) or at an appropriate Mach number. To eliminate altitude effects aircraft
performance calculations are often done at equivalent air speed EAS (see below). Published
data may be quoted at other airspeed definitions. It may be necessary to convert between
the various speeds so it is important to understand airspeed definitions.
The main ones are listed below:-
IAS = 'indicated airspeed'- this is the speed
displayed on the aircraft instruments. As such it is a function of height (static
pressure) and forward momentum (dynamic pressure). The value displayed on the instrument
will be affected by local atmospheric conditions and by errors from the installation of
the sensors on the aircraft.
CAS = 'calibrated airspeed' - this is the speed as
determined by the airspeed indicator corrected for positional and instrument errors. Since
this correction is often done within the instrument in which case the value is often
equivalent to the IAS. However if there are significant interference effect generated by
the airframe a further correction will be necessary to show IAS.
EAS = 'equivalent airspeed'- this is the true
airspeed corrected for altitude effects:-
VEAS = (s)0.5. VTAS
Equivalent airspeed is a direct measure of the kinetic
energy per unit volume of air and therefore is directly related to the forces on the
aircraft (lift and drag) and the corresponding structural loading. The correction of EAS
from CAS depends on the nature of the correction built into the airspeed indicator.
TAS = 'True airspeed'- this is the speed measured
over the ground. The prefix K (KTAS) is sometimes used to indicated that the speed is
quoted in knots.
DYNAMIC PRESSURE (q)- this is used in aerodynamic
equations to link speed to forces on the aircraft.
For example, Lift is defined as (q S CL) (where,
q = 0.5 r (VTAS)2 = 0.5 ro (VEAS)2 ) |