Chapter 1.5: Examining Relationships: Correlations
Often in nature, different variables display similar patterns of variability. As one changes, the other is likely to change in some predictable way (they are said to be related to each other). In the environmental sciences, it is often useful to quantify the strength, nature and significance of these relationships. It helps us to understand how the various components of an ecosystem are interconnected and informs management decisions designed to help mitigate environmental problems. The most common test of relationships is the Pearson’s Correlation (r), which provides a simple metric for quantifying the proportion of variance in common between two continuous variables. When data are not normally distributed, converting your data to ranks and running the Pearson’s calculations will approximate a non-parametric test.
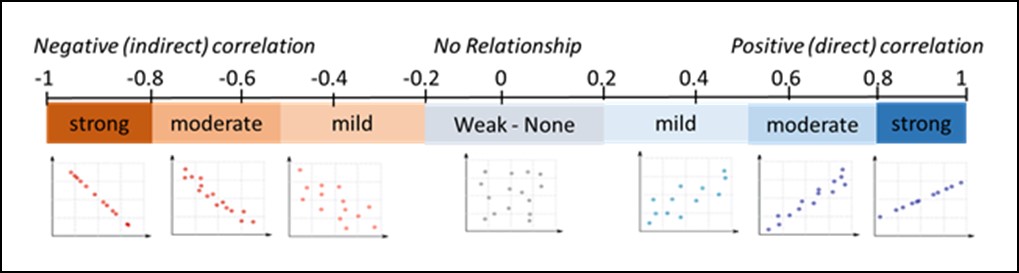
Background Materials:
The basic steps for inferential analyses:
Different groups break it down into different subsets of steps, but the basics remain the same…..note you still have to do all the same things; they just break it down differently. The question is this: are you a lumper or a splitter? Lumpers should try the five steps; splitters should go for the seven:
Hypothesis testing in 5 steps: http://www.nedarc.org/statisticalhelp/advancedstatisticaltopics/hypothesisTesting.html
Hypothesis testing in 6 steps: http://www.unf.edu/~jgleaton/HypSteps.html
Hypothesis testing in 7 steps: http://www.freemathhelp.com/forum/threads/75484-7-step-Hypothesis-testing-yikes!
Fewer steps, and more theory on hypothesis testing: http://www.biostathandbook.com/hypothesistesting.html
The Basics of Correlations:
Correlation for Dummies:
http://www.dummies.com/how-to/content/how-to-interpret-a-correlation-coefficient-r.html
A compilation of great correlation links pulled together by the University of Sheffield:
http://www.mash.dept.shef.ac.uk/Correlations.html
Khan’s take on correlation and causality:
https://www.khanacademy.org/math/probability/regression/regression-correlation/v/correlation-and-causality
An overview of the Pearson Correlation in basic terms from Laerd:
https://statistics.laerd.com/statistical-guides/pearson-correlation-coefficient-statistical-guide.php
….and also for the Spearman’s Rank Correlation:
https://statistics.laerd.com/statistical-guides/spearmans-rank-order-correlation-statistical-guide.php
Textbook References and Links:
Correlation calculators (Note that this just gives you the correlation coefficient once you enter all the data, but it does not give you the associated p-value to assess the significance of that correlation):
Pearson’s: http://www.socscistatistics.com/tests/pearson/
Spearman’s: http://www.socscistatistics.com/tests/spearman/
Correlation p-value calculators (the better way, where you calculate the correlation coefficient yourself and then use this calculator to determine significance). Note that these will work for either the Pearson’s or Spearman’s correlation coefficient. You just need to know your sample size:
http://www.socscistatistics.com/pvalues/pearsondistribution.aspx or
http://www.danielsoper.com/statcalc/calculator.aspx?id=44
Correlation critical value look-up tables. Interested in doing it the old-fashioned way? Just look up your set alpha (significance level in the correct column), and your correct degrees of freedom (to identify the correct row) and see if the correlation coefficient you have calculated exceeds the critical value in the main body of the table:
http://www.biologyforlife.com/correlation.html
Downloadable data and files:
Practice Exercise: These data show decadal mean temperatures and atmospheric CO2 concentrations.
Download Tools examples 1.5.csv


